#Y2025 #定义 Update date: 2025-02-23 参考：[分辨率的七大判据](https://mp.weixin.qq.com/s/Bmqx4y48u_WelnyV4o4Lqg) # 阿贝判据（Abbe Criterion） 阿贝判据是一种常用的分辨率判定标准，最早是由1873年恩斯特·卡尔·阿贝基于“Airy斑”原理提出的，定义了只有当零级和一级衍射都能通过物镜时，才能分辨出相距为d的两个特征。这一判定标准尤其适用于显微镜等高倍率成像系统。根据阿贝判据理论，两个点光源的最小可分辨距离d为：d=λ/2nsinθ，其中，λ是光波长，n是样品与显微物镜之间介质的折射率，θ是显微物镜的孔径角。这一经典的公式也被刻于阿贝墓碑上。阿贝是首位定义数值孔径术语的科学家。阿贝判据强调了数值孔径的重要性，NA=nsinθ，θ表明高数值孔径的物镜可以提高分辨率。 # 瑞利判据（Rayleigh Criterion） 1895年英国物理学家瑞利以“Airy斑”理论为基础，对“Abbe光学衍射极限理论”进行了进一步的延伸和细化。它指出，当两个艾里斑的第一个暗环刚好与另一个艾里斑的中心重合时，这两个点被认为是可分辨的。根据瑞利判据，两个点光源的最小可分辨距离 d 为：d = 1.22λf/D = 0.61λ/NA，这意味着，要分辨两个紧密相邻的点，它们之间的距离必须大于等于艾里斑的半径。瑞利判据提供了一个直观且易于理解的分辨界限，适用于大多数光学系统，包括显微镜、望远镜等成像系统。目前光刻机发展的根本遵循则是瑞利判据，瑞利判据也被光刻产业界奉为“金科玉律”。 # 斯帕罗判据（Sparrow Criterion） 斯帕罗判据于1916年被提出，是关注于合成强度轮廓的二阶导数，当合成强度轮廓的中心是平坦的，说明强度对位置的导数在原点处为零，此时分辨率达到极限。将此条件应用于两个艾里斑的合成强度轮廓，可得到斯帕罗分辨率R(S)=0.47λ/NA。 由于斯帕罗判据可以提供一个更为精细的分辨率评估，因此在天文学中尤为常用。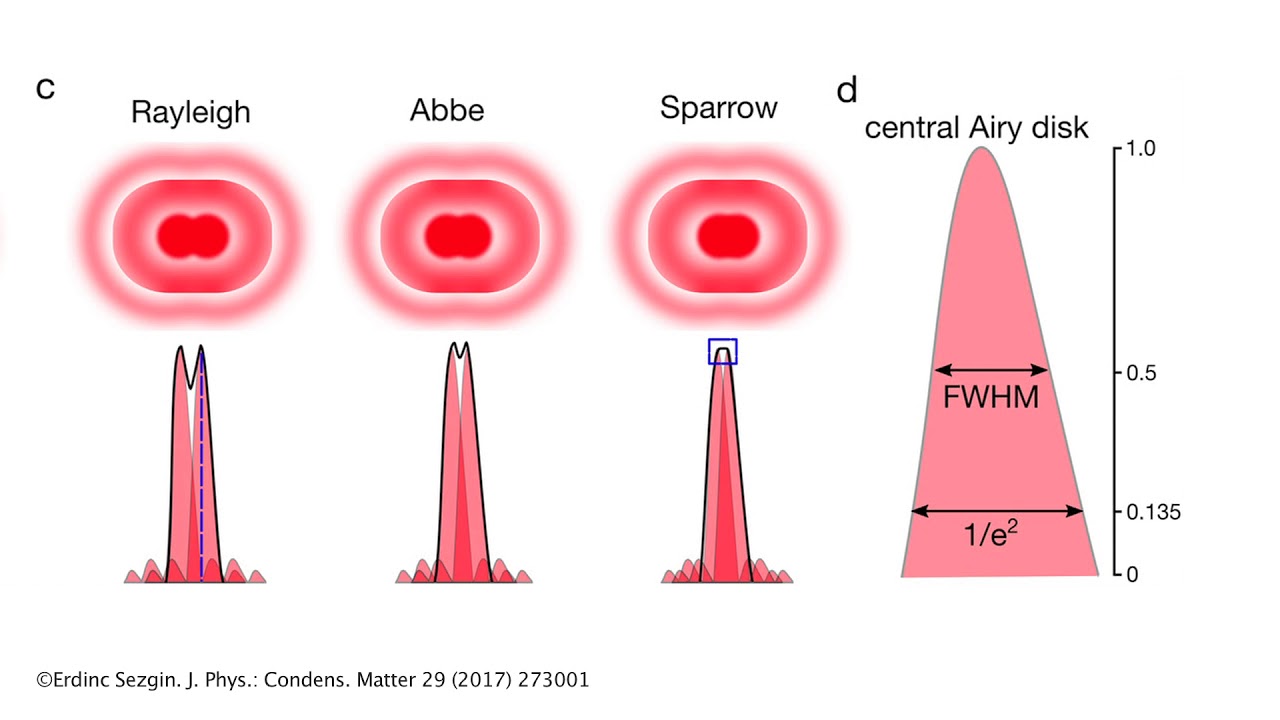 前三种判据的示意图如下：  # 半峰全宽判据（FWHM Criterion） 在光学成像系统中，半峰全宽可以用来描述成像系统的分辨率。当半峰全宽较小时，成像系统的分辨率较高反之，半峰全宽较大时，成像系统的分辨率较低。半峰全宽相对容易用显微镜测量，成为用于比较目的的普遍接受的参数。FWHM的理论值为RFWHM= 0.51λ/（NA），大约是λ/（2NA）。所以FWHM作为分辨率参数非常接近阿贝的衍射极限。使用FWHM的优势在于，它可以在实验室中通过对伪点发射光(例如亚分辨率荧光珠)成像进行实际测量，因此可以用作真实显微镜系统的比较指标，相比之下其他极限理论是理想情况下的。 # 道威判据（Dawes Criterion） 我们知道，某一发光物点经衍射受限系统(指理想的无像差光学系统)成的像为一艾里斑。两个靠得很近的独立发光点的艾里斑，其重叠部分的光强为两艾里斑光强之和。分辨两衍射斑的前提条件是其重叠区的光强对比度K应大于人眼的对比灵敏度。瑞利判据的分辨条件K=15%，斯帕罗判据的分辨条件K=0，而道威判据的分辨条件K=2.6%。道斯认为，当分辨条件K=2.6%时，人眼刚能分辨两衍射斑的中心距为RD=1.02λF。瑞利判据是比较严苛和保守的，实际生产中，往往以道威判据作为分辨率极限的情况居多，通常以道斯判据给出的分辨率作光学系统的目视衍射分辨率(也称为理想分辨率)。 望远镜系统以物方刚能分辨开的两发光点的角距离α表示分辨率，即以望远物镜后焦面上两衍射斑的中心距RD对物镜后主点的张角α表示 # 马雷夏尔判据（Marechal Criterion） 根据Marechal判据,当光学系统的波前误差（RMS）不超过λ/14 时，系统可以认为是衍射受限的，即其性能接近理想情况下的极限。很多时候大家也这么规定，当系统波像差RMS（AVG WFE RMS）小于0.075λ，可以认为它们的像质接近或达到了衍射极限。我们常说的衍射极限即为光学系统的极限分辨率，当光学系统的像差和衍射现象越小时，系统的分辨率越靠近衍射极限，即越接近极限分辨率。 # 斯特列尔比判据（Strehl Ratio Criterion） 斯特列尔比是用来比较光学系统实际性能与其衍射极限性能的指标,它综合反映了光学系统的波前误差和成像质量，对于评估和优化光学系统设计具有重要的意义。它定义为实际光学系统产生的点扩散函数(PSF)的峰值强度与理想衍射受限系统（即完美系统，没有任何像差）的PSF峰值强度之比。斯特列尔比可以量化由于波前误差（如光学畸变、大气扰动等）导致的成像质量下降。当光学系统有像差时，艾里斑占有的光强度比理想时的低。两者的强度比为斯特列尔比。完美无像差时，S=1。明确的像差类型决定了准确的斯特列尔比，Maréchal发现，对于任何像差，斯特列尔比的极限总是接近0.8，所以当斯特列尔比大于0.8时，也可认为系统接近衍射极限。 --- 版权声明: 感谢您的阅读，本文由[超光](https://faster-than-light.net/)版权所有。如若转载，请注明出处。